图形学基础
线性代数基础
向量
- 用$\vec{a} 或者 \pmb{a}$表示向量,$\hat{a} = \frac{\vec{a}}{|\vec{a}|} $,表示单位向量
- 向量的坐标形式,列向量$\vec{a} = \begin{pmatrix} x \ y \ z \end{pmatrix}$
- $\pmb{a}^T = \begin{pmatrix} x & y & z \end{pmatrix} , 转置运算$
- 向量的运算:
- $\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|cos\theta,其中\theta为向量\vec{a},\vec{b}的夹角$
- $\vec{a} \times \vec{b} = - \vec{b} \times \vec{a},|\vec{a} \times \vec{b}| = |\vec{a}||\vec{b}|sin\theta$
对于 $\vec{a} \times \vec{b} $ 必然可以转换成矩阵和向量的乘积,相当对于向量的旋转即 $\pmb{a} \times \pmb{b} = C\pmb{b}$
对于$\pmb{a} = \begin{pmatrix} x_a \ y_a \ z_a \end{pmatrix},\pmb{b} = \begin{pmatrix} x_b \ y_b \ z_b \end{pmatrix} , \pmb{a} \times \pmb{b} = C\pmb{b} = \begin{pmatrix} 0 & -z_a & y_a \ z_a & 0 & -x_a\ -y_a & x_a & 0\end{pmatrix}\begin{pmatrix} x_b \ y_b \ z_b \end{pmatrix} = \begin{pmatrix} y_az_b-y_bz_z \ z_ax_b-x_az_b \ x_ay_b-y_ax_b \end{pmatrix}$
- 向量运算的应用:
- 投影变换
- 向量相对位置的确定
- 点是否在图形内部的确定
矩阵
- 对于矩阵的定义不在给出(读者可以自行查询)
- 矩阵乘法:$M{n\times m} * N{m \times t} = A_{n \times t}$
★图像变换
主要的目的:3D World $\rightarrow$ 2D Image
2D的变换
缩放反转

下面的公式便是代表了2D图像的缩放
这个公式代表了对在x轴方式向上缩放$S_x$倍,对在y轴方式向上缩放$S_y$倍
对于图像的反转,可以对$S_x = -1 或者 S_y = -1$操作方式与缩放完全一样
切变(shear)

下面的公式代表了上方2D图像的切变
旋转(Rotate)
默认来说,都是关于原点(0,0)选择,不在原点旋转的可利用平移转化,并且默认为逆时针旋转
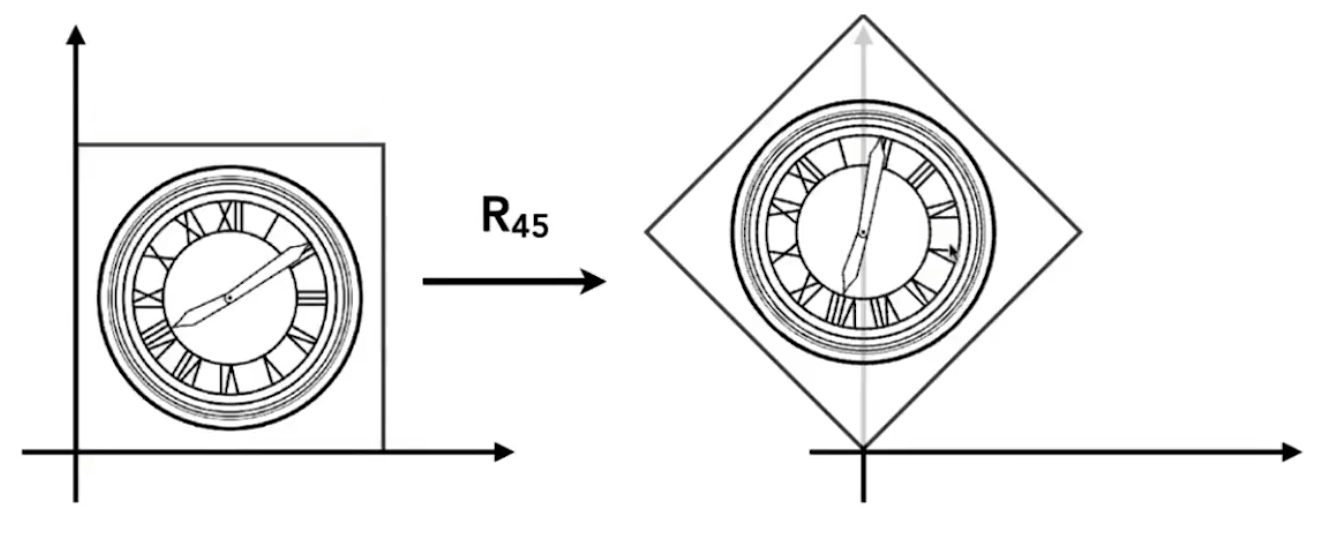
旋转矩阵的结果,记住就可以了
平移
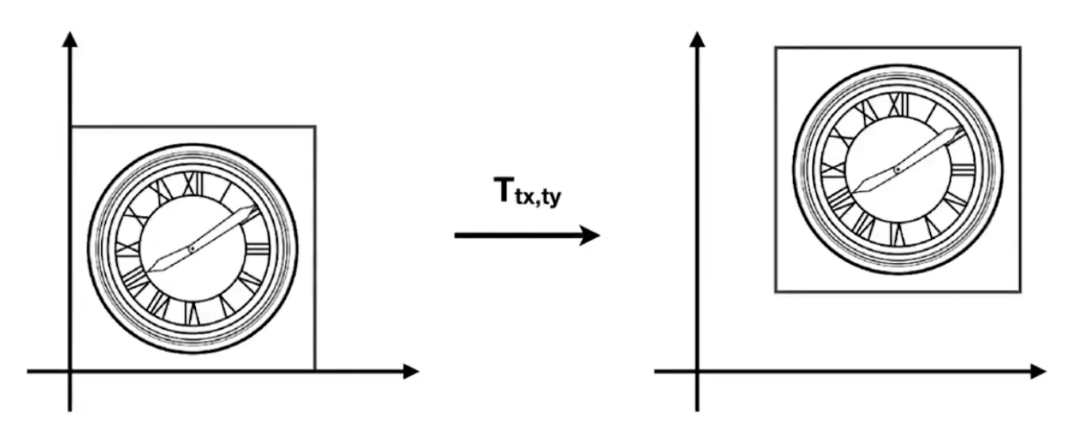
但是对于平移出现了一个问题,无论如何变形,对于 上述的变形式子 无法变为$ \pmb{x’} = D\pmb{x}$的形式,这个问题会在下一节中展示
对于$ \pmb{x’} = D\pmb{x}$形式的
齐次线性变换
为了更好的表示齐次线性表示所有的变换,为了不让平移变成一个特殊,我们在每个向量或者点添加一维元素如下表示:
- $ 2Dpoint = (x,y,1)^T $
- $2D vector = (x,y,0)^T$
这次可以利用以下公式对于线性变换表示平移:
对于前面说的缩放反转、切变、旋转都可以用扩展后的矩阵进行齐次变换只需要如下公式:
缩放 $\mathbf{S}\left(s_x, s_y\right)=\left(\begin{array}{ccc}s_x & 0 & 0 \ 0 & s_y & 0 \ 0 & 0 & 1\end{array}\right)$
旋转 $\mathbf{R}(\alpha)=\left(\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0 \ \sin \alpha & \cos \alpha & 0 \ 0 & 0 & 1\end{array}\right)$
注意:$\mathbf{R}(-\alpha)=\left(\begin{array}{ccc}\cos \alpha & \sin \alpha & 0 \ -\sin \alpha & \cos \alpha & 0 \ 0 & 0 & 1\end{array}\right) = \mathbf{R}(\alpha)^{-1} = \mathbf{R}(\alpha)^T$
- 平移 $\mathbf{T}\left(t_x, t_y\right)=\left(\begin{array}{ccc}1 & 0 & t_x \ 0 & 1 & t_y \ 0 & 0 & 1\end{array}\right)$
对于前两个,我们发现,仅仅用我们之前推导的$2\times2$的变换矩阵,替换这个$3\times3$的矩阵的左上方的$2\times2$的格子即可,对于平移我们只要在单位矩阵的第三列前两个元素添加平移的距离即可完成变换
由于变换具有组合性,故对于一个变换都可以分解成多个基础齐次线性变换,所以对于一个变换矩阵M,都可以分解成上述的S、R、T的乘积,例如
代表先对图像逆时针旋转45°再平移(1,0)的距离
此时我们可以知道$M = T{(1,0)} \cdot R{45},M代表整个过程的变换矩阵$
非原点变换
一句话,平移至原点再变换。例如下图,

3D的变换
类比于2D的变换,我们也可以类比2D齐次变换
- $ 3Dpoint = (x,y,z,1)^T $
- $3D vector = (x,y,z,0)^T$
对其线性变换如下公式:
对于这种扩展点的定义,我们也可以扩充至$\omega \neq 1,0$的情况,对于$(x,y,z,\omega),\omega \neq 0 代表真实点(x/\omega,y/\omega,z/\omega) $
思考:对于应用上面的3D的齐次线性变换的变换矩阵,变换时是先平移还是先旋转(或者线性变化)呢 ?
*答:先进行线性变换,再平移*对于上面的相关的变换矩阵性质可以类比于2D变换的矩阵性质
特殊的旋转矩阵
围绕x-、y-、z-轴旋转,如下矩阵:
因此对于欧拉角我们可以这样转换为矩阵: $\mathbf{R}_{x y z}(\alpha, \beta, \gamma)=\mathbf{R}_x(\alpha) \mathbf{R}_y(\beta) \mathbf{R}_z(\gamma)$ 一般旋转
非欧拉角旋转矩阵求法
默认旋转轴过原点
3D转换成2D
view变换
- 观测点位置(拍照位置)==== 默认(0,0,0)
- 观察方向(拍的方向)==== 默认 向-z的方向看
- 观察点旋转方向(相机旋转的方向)==== 默认 向上方向是y轴方向
将一个一般观测点转化成上述默认方向
- 先将位置平移到原点
- 在旋转到默认方向
- 变换矩阵$\mathbf{M} = R{view} T{view}$
Projection变换
3D转2D的关键步骤
正交投影
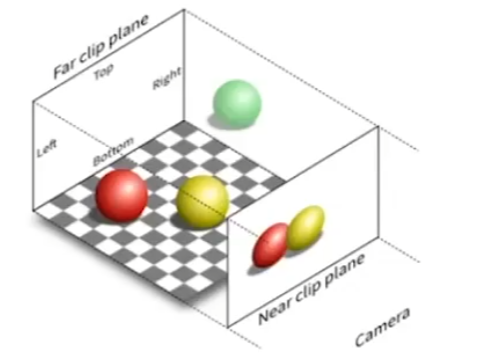
变换:直接去掉某一面的坐标元素量
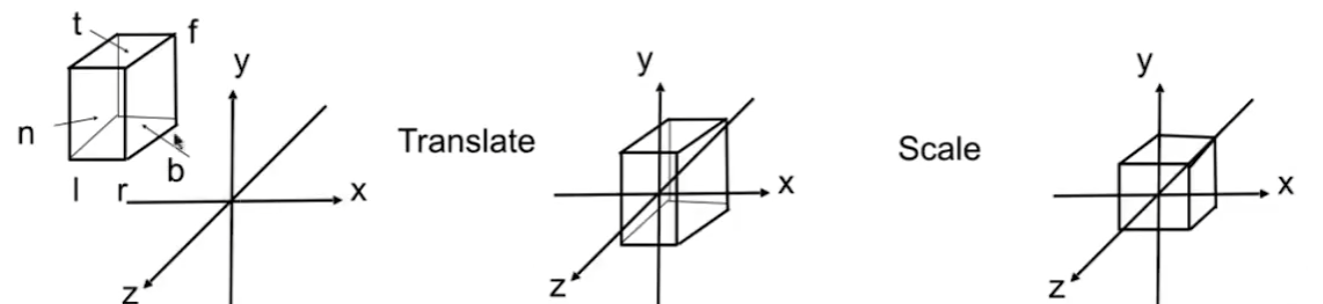
我们定义一个长方体$[l,r]\times[b,t]\times[f,n]$
映射到坐标$[-1,1]^3$上,规范化,映射矩阵如下(先平移,再缩放)
透视投影
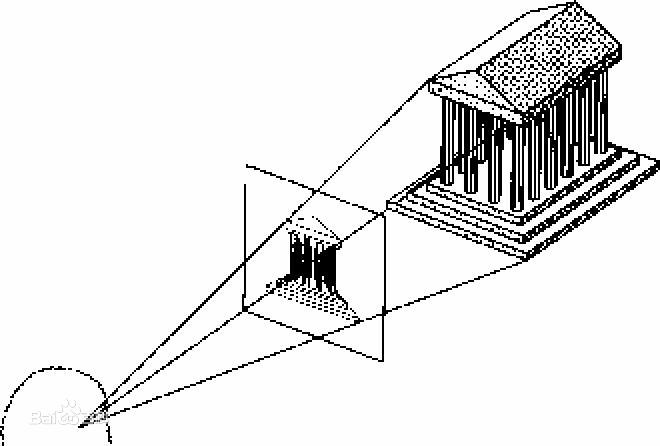
回顾:对于$(x,y,z,1)与(kx,ky,kz,k),k\ne0$表示为同一个点
透视投影完成的步骤:
- 先收缩f处的画面(远近的间距不变、图像中心点不变) $M^{(4\times4)}_{presp \rightarrow ortho}$
将收缩后的画面正交投影到n处 $M_{\text {ortho }}$
透视变换矩阵 $M{presp} = M{ortho} \cdot M_{presp \rightarrow ortho} $
通过一定的推导我们可以求解到压缩变换矩阵 推导过程
思考:对于远近平面挤压时,对于其z值挤压前后不变,那么除了f、n两处的面,其他的面挤压前后的z应该是怎样变换?(n~f之间的面) 答案解析