Z-buffer

画家算法：渲染由远到近，近处覆盖远处(对于多层三角形的互叠不可用)

一般不透明三角形深浅度表示，浅的盖住深的部分

深度缓存算法：

for(each triangle T)
    for(each sample(x,y,z) in T)
        if(z<zbuffer[x,y])
            framebuffer[x,y] =rgb
            zbuffer[x,y]=z
        else
            ;

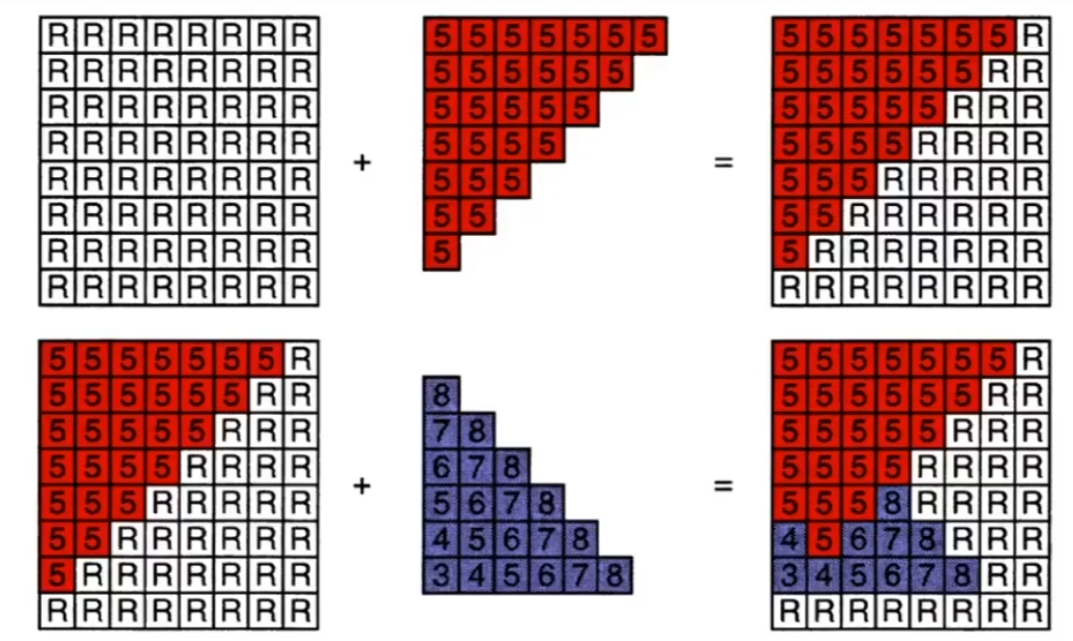
z-buffer算法图示

$R$代表无限大，初始化z-buffer为全部元素为$R$

Shading

作用：引入颜色明暗的过程，在不同材质引入不同的影像

Blinn-Phong Reflectance Model

三种光照情况

Specular highlights：高光部分

Diffuse reflection：漫反射

Ambient lighting：环境光照

计算光反射的部分：

着色这里不考虑其他物体的存在

Inputs
- 观测方向 $\mathbf{v}$
- 法线方向 $\mathbf{n}$
- 光照方向 $\mathbf{l}$
- 其他参数(颜色参数、光照强度参数等) 以及 shading point 的参数(材质等)

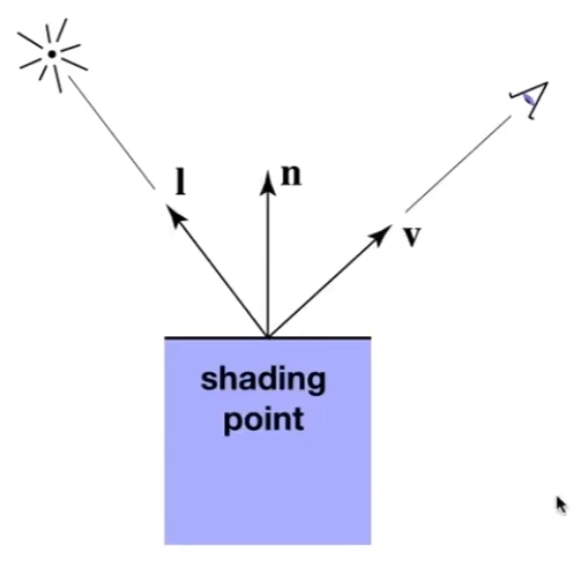
仅代表方向的向量均为单位向量

漫反射(diffuse reflection)

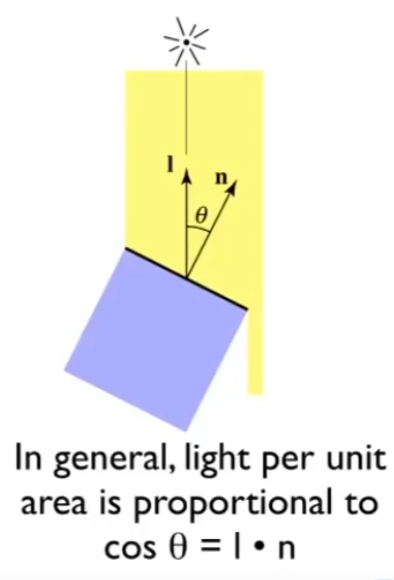
单位面积得到的光的能量

这里利用光源与法线方向的点积结果可以作为角度权重

根据能量守恒，我们可以假设光源发出的能量均匀的分布于以光源为圆心的圆壳上，那么对于随着光的传播，在球壳上的单位面积上的能量将会减小。

$P \propto \frac{I}{r^2}$

P代表单位球壳上的光强能量，r代表球半径，I代表总光强能量

根据上面的推导，我们可以拿到总的公式，（注意，这个只是一个经验模型，并不是实际物理模型）

$L_d = k_d(I/r^2)max(0,\mathbf n \cdot \mathbf l)$

这里$L_d$漫反射的光强权重，$k_d,k_d \in [0,1]$ 表示材质对光强的吸收，$k_d$越大说明材质对于该光线的吸收度越小

漫反射的各个参数的影响

$k_d$ 的只是表示一个漫反射的参数，但是对于上述的模型可能会存在一定的整数倍的参数，导致不再满足$k_d \in [0,1]$ 这里还是那句话，这只是一个经验模型，没有经过物理实验严谨的实验；对于上述的对比图也是证明了这个经验有一定的可信性

高光项(specular highlights)

引入一个半程向量用$\mathbf{h}$表示

$\mathbf h = bisector(\mathbf v , \mathbf l) = \frac {\mathbf v + \mathbf l} {|\mathbf v + \mathbf l|}$

根据上一节漫反射的推到我们可以得到另一个经验模型参数：

$\begin{aligned} L_s &= k_s(I/r^2)max(0,\cos{α})^p\\ &= k_s(I/r^2)max(0,\mathbf n \cdot \mathbf h)^p \end{aligned}$

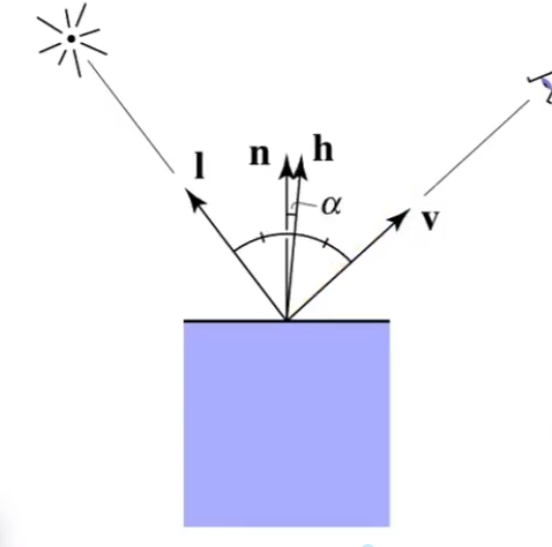
高光项图像解析

$\mathbf n$和$\mathbf h$ 的接近可以反映成观测方向和反射方向的相似性
对于夹角上的p指数，是为了缩小对于高光项的角度范围，为了更好的模拟高光项，我们尽可能对于观察到高光项的角度进行所见，其中对于$\cos^p \alpha $ 对于p的变化可如下图所示

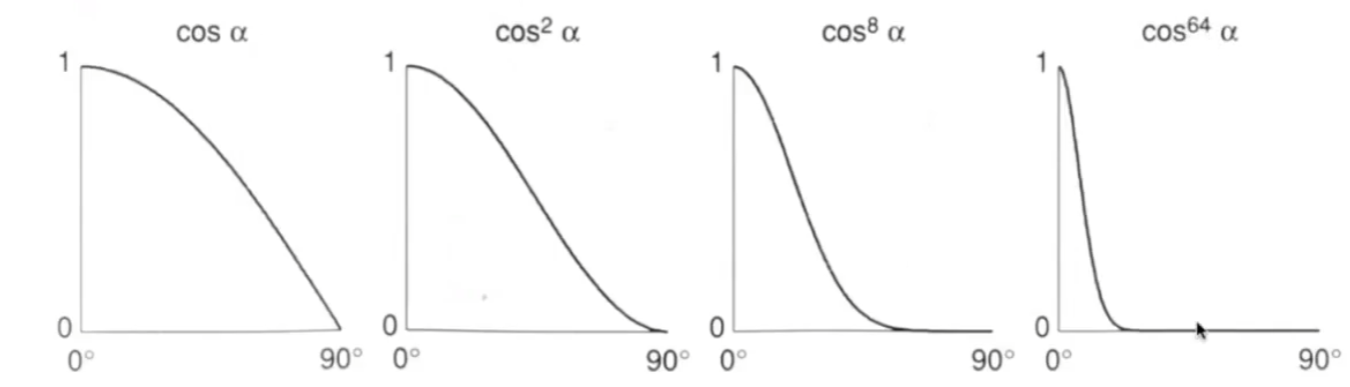
cos值随指数变化对比图

我们明显看出，对于随着p的增加，观测到高光的角度范畴逐渐减小。p对于可视图像的影响如下图

参数对于结果的影响

环境光照(Ambient lighting)

对于环境光照我们现在可以用一个常数进行表示

这里可以用 $ L_a = k_aI_a$来表示这个值

$k_a$为环境光照系数，$I_a$为环境光照强度

通过上述的三个部分的介绍，我们可以将光照强度叠加得到我们最后的模型

$\begin{aligned} L &= L_a + L_d + L_s \\ &=k_aI_a + k_d(I/r^2)max(0,\mathbf n \cdot \mathbf l) + k_s(I/r^2)max(0,\mathbf n \cdot \mathbf h)^p \end{aligned}$

图像的叠加可以参考下面的一张图片

三个部分的叠加的结果图

Shading Frequencies

着色频率: 确定颜色渲染的点的位置，具体的变化如下图展示

着色频率的实例

第一个，按每个四边形着色；第二个，按每个四边形的顶点进行着色；第三个，按每个像素进行着色，对应下面的三种着色方式：

Flat Shading —— 频率按面(face)
Gouraud shading —— 频率按点(vertex)
Phong shading (效果最好) ——频率按像素(pixel)

三种方式的对比，如下图

三种着色的方法对比

补充：

定义顶点的法线：①对于顶点关联的所有面求法向量在叠加平均 ②对于顶点关联的所有面求法向量根据每个面的面积求加权平均叠加

定义像素的法线：见之后的笔记

Graphics(Real-time Rendering) Pipeline

图形渲染管线（实时渲染管线）

图像渲染管线的步骤

着色器(Shader Programs)

vertex
fragment or pixel

Example GLSL fragment shader program

uniform sampler2D myTexture;
uniform vec3 lightDir;
uniform vec2 uv;   // uv代表纹理位置轴
varying vec3 norm;

void diffuseShader(){
    vec3 kd;
    kd = texture2d(myTexture,uv);
    kd* = clamp(dot(-lightDir,norm),0.0,1.0);
    gl_FragColor = vec4(kd,1.0)
}

着色器的编程不需要进行循环，只需对一个像素或者顶点的染色代码即可

推荐网站 Shadertoy : 着色器的编写练习的网站

Texture Mapping

纹理映射：不希望每个点都是一样的颜色，应该对于每一个点都要有自己的特定的属性

前提：3D（实体）的一个点一定可以对应到一个2D（纹理）上的一个点

纹理效果渲染

★ 纹理插值

重心坐标理解

如何利用三角形三个顶点表示三角形内的任意一个点的坐标

假设三角形在▲ABC中，A、B、C的坐标已知，我们可以利用如下思想表示

$(x,y) = \alpha A + \beta B + \gamma C,\alpha + \beta + \gamma = 1，$

便可以转化坐标：

$(x,y,z) \Rightarrow (\alpha,\beta,\gamma)$

这种思想中若有条件$\alpha,\beta,\gamma \geq 0$时，表示的点必然在三角形内部或边缘

使用中心坐标做纹理插值

$V = \alpha V_a +\beta V_b + \gamma V_c$

其中$V_a,V_b,V_c$可以是位置、纹理信息、深度、色彩等

三维中的属性，在三维中做插值再把对应的属性投影到二维中

纹理应用

伪代码示例

1
2
3

(u,v) = evaluate texture coordinate at(x,y)
texcolor = texture.sample(u,v);
set sample's color to texcolor; // 这里通常是上面所说的 漫反射常数kd

对于uv的理解，本文中设计比较少，可以通过百度词条进行理解

双线性插值(Bilinear)

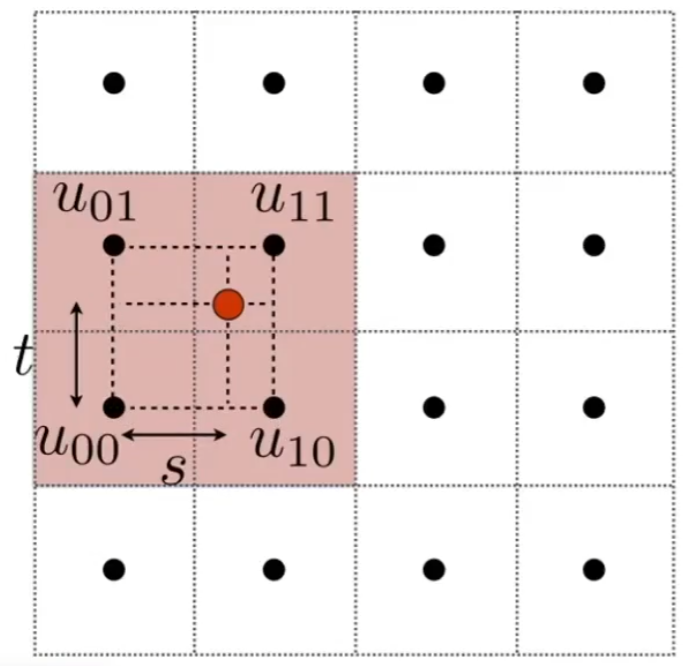
双线性插值

根据图示进行插值计算

水平方向的插值

$u_0 = lerp(s,u_{00} - u_{10}) \\ u_1 = lerp(s,u_{10} - u_{11})$

垂直方向的插值

$f(x,y) = lerp(t,u_0,u_1)$

插值公式: $lerp(x,v_0,v_1) = v_0 + x(v_1 - v_0)$

Bicubic插值

课上没讲，我也没查

三种插值的方法对比

Nearest ：不做插值，一个方格颜色是一样的
Bilinear ：双线性插值
Bicubic ：三重多次插值

点查询 vs 范围查询

由于每个像素的范围的大小不同，这里就要用到范围查询

Mipmap

图像生成

这里的的存储量的计算方法计算就是对等比数列求和

$B = 1 + (\frac{1}{2})^1 +(\frac{1}{2})^2+ \ldots = \lim_{n \rightarrow \infty} \sum_{i=0}^n(\frac{1}{2})^i = \frac{4}{3}$

三线性插值

三线性插值的过程

先对D层进行双线性插值
在对高一D+1层进行双线性插值
最后对两次之间进行插值,得到D层插值数

Mipmap Limitation

Mipmap的缺陷

远处的部分已经过度的模糊了

解决方法：各向异性过滤 或者 EWA过滤