几何图形
几何图形简介
几何图形的表示
隐式函数表示
例如:$f(x,y,z) = x^2+y^2+z^2-1,f(x,y,z) = 0$ 都隐式的表示一个球面,但对于每一个$(x,y,z)$来说都是不直观的,但是对于每一个相对于球面的位置都可以很容易根据$f(x_1,y_1,z_1)$的值判断$(x_1,y_1,z_1)$在球面的内部还是外部
优点:不直观
缺点:可以很容易的确定点与面的关系
隐式函数的有点总结:
- 描述起来比较简单
- 某些查询很容易(对象内部,到表面的距离)
- 适合于光线和表面的求交
- 对于简单的形状,精确描述/无采样误差
- 适合用来描述拓扑结构(如流体)
显示函数表示
例如:$f(u,v) = ((2+\cos u)\cos v,(2+\cos u)\sin v,\sin u)$表示一个面。可以根据$(u,v)$很容易得到一个确认的$(x,y,z)$的点
- 优点:可以很快的写出曲面上的任意一个点,直观
- 缺点:不好判断空间中的任意一点与面的关系
集合思想表示(CSG)
通过集合的布尔运算进行运算,如下图:

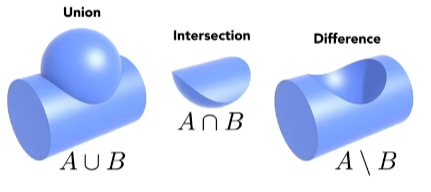
通过对于简单的几何图形进行集合运算我们可以完成对于一些复杂几何模型的组合,相比于上面的隐式和显式的数学表达式来表示几何图形,更加立体直观。
距离函数表示*
对于任何一个几何都不直接去描述它的表面,而去表述任何一个点到这个表面的最近距离。距离函数是指空间中任何一个点到需要表达的几何形体之间的最小距离。如果有一个点在几何形体的外面则距离是正数,如果有一个点在几何形体的里面则计算出最小距离后加一个负号。空间任何一个点都有一个距离值,把这两个物体各自的距离函数都算出来之后,把两个距离函数做一个融合,再把他恢复成原来的物体。
分型表示※
分形类似于递归
例如雪花是六边形的,放大后每一条边上还有六边形,六边形里面仍然还有六边形。
曲线和曲面
obj文件的组成:
1 | v:顶点信息 |
曲线
贝塞尔曲线
贝塞尔曲线(Bezier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。
贝塞尔曲线的一些特性:
- 使用$n$个控制点${P_1,P_2,…,P_3}$来控制曲线的形状
- 曲线通过起始点$P1$和终止点$P_n$,接近但不通过中间点$P_2 \sim P{n-1}$
公式理解
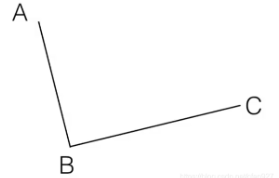
step 1.在二维平面内选三个不同的点并依次用线段连接
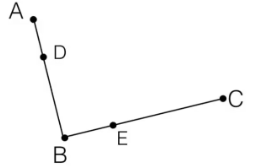
step 2.在线段$AB$和$BC$上找到$D、E$两点,使得$\frac{AD}{BD} = \frac{BE}{CE}$
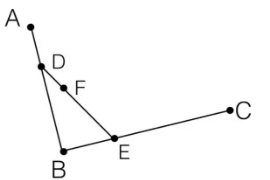
step 3.连接$DE$,并在$DE$上找到$F$点,使其满足$\frac{DF}{EF} = \frac{AD}{BD} = \frac{BE}{CE}$
step 4.找出符合上述条件的所有点
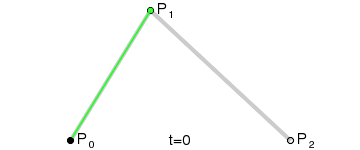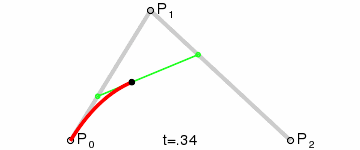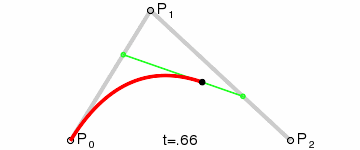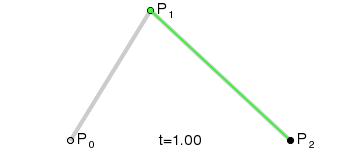
对于具体的公式以及对于相关的多阶的贝塞尔曲线的如下:
类似于二项式展开的模式
对于推导的过程,之后的文章中可以看到
| 曲线阶数 | 图示 |
|---|---|
| 1阶 | 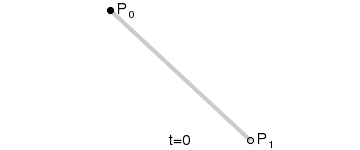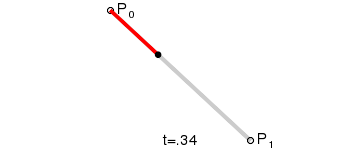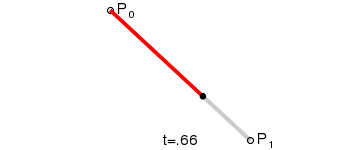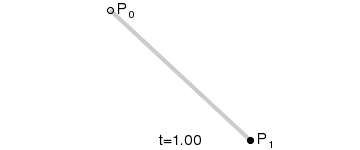 |
| 3阶 |  |
| 4阶 | 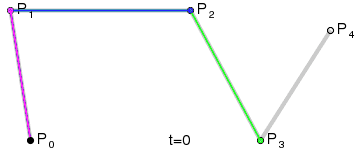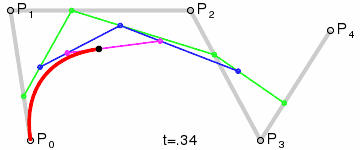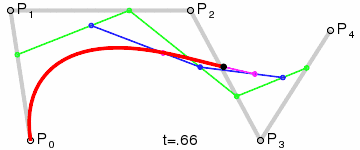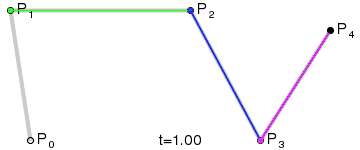 |
| 5阶 |  |
曲面
贝塞尔曲面
其实在理解了贝塞尔曲线之后,贝塞尔曲面的原理也是十分容易理解的了,无非是一个从2维到3维的过渡。

如果说对于曲线来说只有一个参数 $ t\in[0,1]$那么对于一个面来说,就应该有两个参数,分别设$u\in[0,1],v\in[0,1]$,具体过程如下图所示: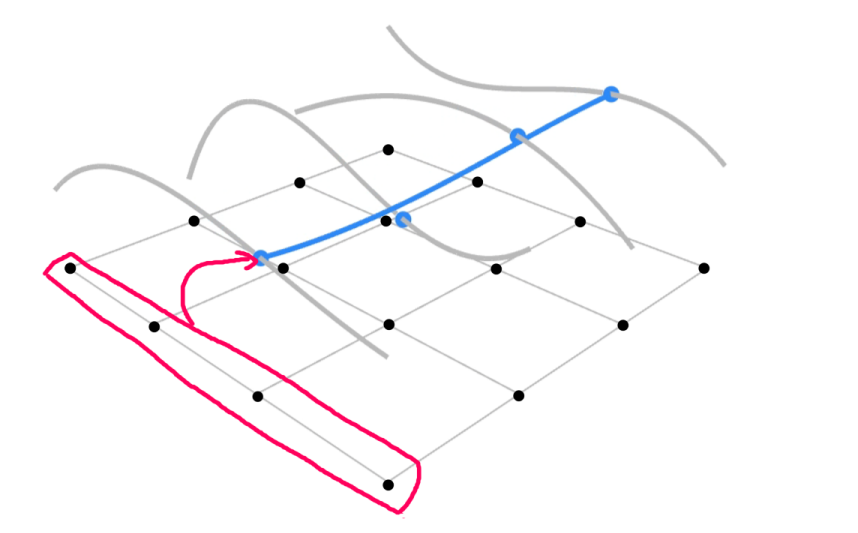
首先规定一共4x4 = 16个控制点,其水平面位置如图中16个黑点所示(并未表示出高度,防止图形太乱),将这16个点分成4列,图中红色圈中的为一列的具体例子。
第1步 在这4个控制点之下利用第一个参数$ u$ 运用计算贝塞尔曲线的方法得到蓝色点,因为有4列,所以一共可以得到如图所示的4个蓝色点。(灰色曲线分别为每列4个点所对应的贝塞尔曲线)
第2步 在得到4个蓝色顶点之后,在这四个蓝色顶点的基础之下利用第二个参数 $v$便可以成功得出贝塞尔曲面上的正确一点
第3步 遍历所有的 $u,v$ 值就可以成功得到一个贝塞尔曲面
几何处理
几何细分
Loop细分
需要三角形Mesh
步骤:
create more triangles (vertices)
Split each triangle into four
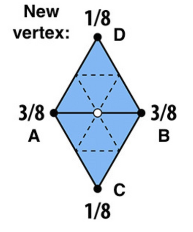
tune their positions (形状需要有改变)
Assign new vertex positions according to weights
New / old vertices updated differently 新老点分别改变
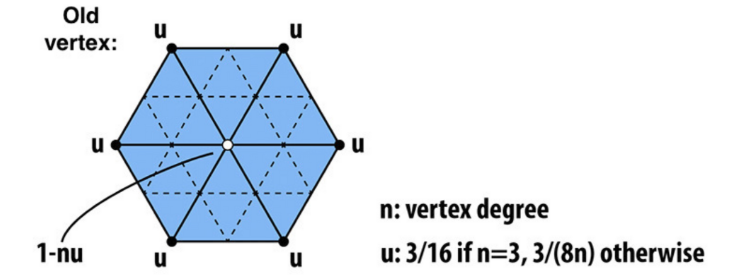
Catmull-Clark 细分
通用Mesh
Non-quad face:非四边的面
Extraordinary vertex (奇异点):指(degree != 4)的点
Each subdivision step:
- 在每个面中添加顶点
- 在每条边上添加中点
- 连接所有新顶点



奇异点在第一次细分增加[非四边形面数量],后续不变;所有非四边形面在第一次细分都会消失
Update Rules (Quad Mesh):

几何简化
目标:减少网格单元的数量,同时保持整体形状
应用:移动端、远距离(LOD)
几何的层次结构
边缘折叠:顶点合并
- 哪些边合并?如何合并?
- Quadric Error Metrics(⼆次误差度量)放在二次误差之和最小的地方
通过二次误差进行简化
- 以最小分数迭代折叠边缘
- 有问题,一条边的操作会影响其它边,需要更新
- 数据结构:优先队列 or 堆
- 贪心算法,非全局最优
- 可以有的放矢



