图像处理以及边缘检测

图像梯度

★ 对于梯度的运算就是卷积的运算的过程 ★

Sobel算子

算子核矩阵如下：

$G_x = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} * A \qquad G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} * A$

注意这里并不是一成不变的，Sonbel核的大小会影响它对核值的改变

类似于高斯滤波，近的位置对于中心点影响大，远的位置影响小
上述可以看出，对于梯度变换黑到白的变换梯度为正，白到黑的变化梯度为负
代码演示

sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)   # 这里因为在展示的时候，会把负数部分覆盖，于是我就要先取绝对值在展示
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
sobely = cv2.convertScaleAbs(sobely)
sobelxy1 = cv2.addWeighted(sobelx, 0.5, sobely, 0.5, 0)
sobelxy2 = cv2.Sobel(img, cv2.CV_64F, 1, 1, ksize=3) # 直接算x,y方向的卷积远没有分开之后算在相加的结果好，所以我们要避免直接计算
sobelxy2 = cv2.convertScaleAbs(sobelxy2)

Scharr算子

算子核矩阵如下：

$G_x = \begin{bmatrix} -3 & 0 & 3 \\ -10 & 0 & 10 \\ -3 & 0 & 3 \end{bmatrix} * A \qquad G_y = \begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ 3 & 10 & 3 \end{bmatrix} * A$

代码展示

scharrx = cv2.Scharr(img, cv2.CV_64F, 1, 0)
scharry = cv2.Scharr(img, cv2.CV_64F, 0, 1)
scharrx = cv2.convertScaleAbs(scharrx)
scharry = cv2.convertScaleAbs(scharry)
scharrxy = cv2.addWeighted(scharrx, 0.5, scharry, 0.5, 0)

Laplacian算子

算子核矩阵如下：

$G = \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}$

代码展示

1 2	laplacian = cv2.Laplacian(img, cv2.CV_64F) laplacian = cv2.convertScaleAbs(laplacian)

算子对比

代码如下

img = cv2.imread('../img/2.jpg', cv2.IMREAD_GRAYSCALE)
img = cv2.resize(img, (400, 400))

sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)
sobely = cv2.convertScaleAbs(sobely)
sobelxy = cv2.addWeighted(sobelx, 0.5, sobely, 0.5, 0)

scharrx = cv2.Scharr(img, cv2.CV_64F, 1, 0)
scharry = cv2.Scharr(img, cv2.CV_64F, 0, 1)
scharrx = cv2.convertScaleAbs(scharrx)
scharry = cv2.convertScaleAbs(scharry)
scharrxy = cv2.addWeighted(scharrx, 0.5, scharry, 0.5, 0)

laplacian = cv2.Laplacian(img, cv2.CV_64F)
laplacian = cv2.convertScaleAbs(laplacian)

res = utils.figure_splicing((img, sobelxy, scharrxy, laplacian))
utils.show_image('res', res)

三种算子的对比

第一个是原图，第二个是Sobel，第三个是Scharr，第四个是Laplacian

边缘检查

Canny边缘检测

使用高斯滤波器，以平滑图像，滤除噪声（已解决）
计算图像中每个像素点的梯度强度和方向（已解决）
应用非极大值抑制，以消除边缘检测带来的杂算响应
应用双阈值检查来确定真实的和潜在的边缘
通过抑制孤立的弱边缘最终完成边缘检查

非极大值抑制

非极大值抑制线性插值法

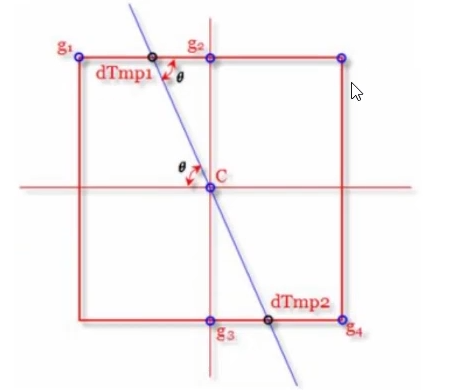
线性插值：设$g_1$的梯度幅值为$M(g_1)$，设$g_2$的梯度幅值为$M(g_2)$，那么对于$dTmp_1$的亚像素的梯度复制为

$M(dTmp_1) = wM(g_2)+(1-w)M(g_1)$

其中$w = \frac {distance(dTmp_1,g2)}{distance(dTmp_1,g2)}$,$distance(x,y)$代表$x$到$y$的距离

简化方法

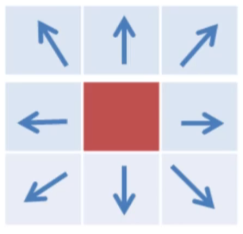
简化的线性插值的算法

为了简化计算，由于一个像素周围共有8个像素，把一个像素的方向离散成八个方向，这样就只需要计算前后的即可，不应插值了

双阈值检查

双阈值检查图示

梯度值 > maxVal : 处理为边界
minVal<梯度值<maxVal : 连有边界的保留，否则舍弃
梯度值 < minVal : 舍弃

代码展示

img = cv2.imread('../img/2.jpg', cv2.IMREAD_GRAYSCALE)
img = cv2.resize(img, (600, 400))
v1 = cv2.Canny(img, 80, 150)
v2 = cv2.Canny(img, 50, 100)

res = utils.figure_splicing((v1, v2))
utils.show_image("11", res)

运行结果：

最后运行结果的对比

对于阈值设置的大小我们可以发现这个，对于越大的的阈值范围（如图一）得到的细节越少杂讯点也少，而对于阈值范围越小的检测（如图二），得到的细节比较多但是同时加剧了得到杂质点的可能