WGAN

WGAN

对于原始的GAN，目标函数涉及到了一个JS散度，这个在训练的时候会出现一个很麻烦的事情。我们首先来回顾一下我们在原始GAN中最终要优化的目标函数：

$$\begin{aligned} C(G) &=\max _D V(G, D)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_g}\left[\log \frac{p_g(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right] \end{aligned}$$

再观察一下，当 $p_{data}$ 分布和 $p_g$ 分布，完全没有交集，或是说只有很狭窄的一个交际（在这高维空间中是很容易得到的情况），我们会和容易发现这个目标函数一个特点: 目标函数是一个常数 ！

这一点非常重要，这不会体现在训练过程中的loss显示，对于两个毫无关系的分布，我们无法在训练的时候观察到模型学习后的分布是不是再向着我们需要的方向优化

下图是论文对于两个分布所做出的JS散度值的一个图像

WGAN算法

为了解决上述提出的问题，我们需要一个新的目标函数来优化这个训练的过程，为此这篇文章提出了一个Wasserstein距离来描述两个分布之间的距离，具体描述如下进行过解释：

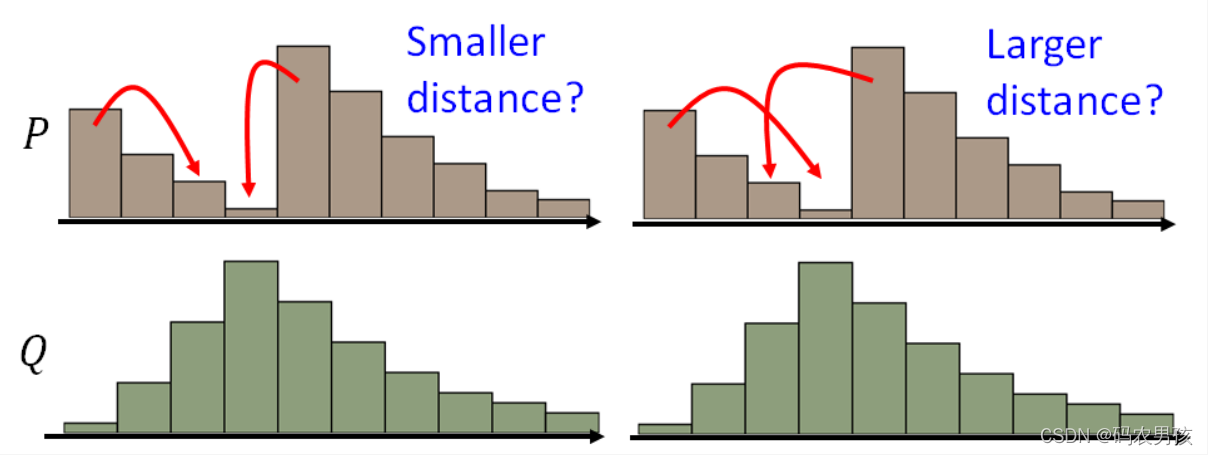
最好的移动方案：

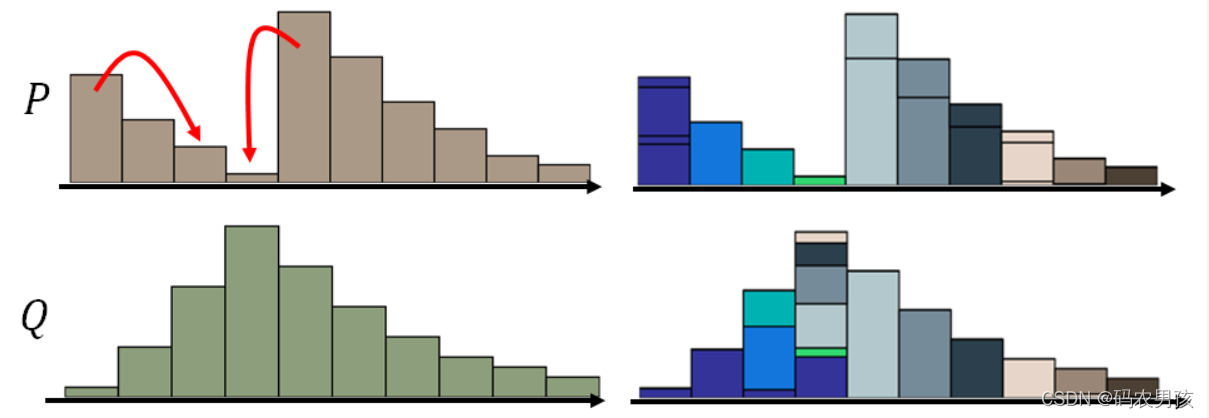
我们把上述图示所展示的“推土机”距离的最好方案定义为Wasserstein距离，这样的话，无论两个分布距离有多么远，这个距离都是存在梯度的，可以用于优化更新。

新的问题来了，如何计算这个Wasserstein距离 ？我们直接给出公式（PS. 这个公式的推导我也不太会）

$$\max _{D \in 1-\text { Lipschitz }}\left\{E_{x \sim P_{\text {data }}}[D(x)]-E_{x \sim P_G}[D(x)]\right\}$$

注意到一个小细节, 对$D$有一个限制 $D \in 1-\text{Lipshitz}$ （或者 $D \in k-\text{Lipshitz}$ )，可视为 $D$ 为平滑的函数（不可以变化过于剧烈）；

为什么要对 $D$ 进行平滑限制？ 如果不加 $D \in 1-\text{Lipshitz}$ 的限制，最后我们会看到这个Wasserstein距离会趋近于无穷大，无法收敛。

$D \in 1-\text{Lipshitz}$ 的实现 ：对于这个限制实现，就是要求 $D$ 的变化率不可以很大，即再小范围内 $D$ 的变化不可以过于剧烈