pix2pix

论文主页 Image-to-Image Translation with Conditional Adversarial Networks

简介

pix2pix算法是解决对于图像域转换翻译问题的奠基地位的一个算法。其中有很多方面的应用（开篇的链接中已经展示实例）

效果展示

理论基础

pix2pix算法实际上是在条件对抗网络(cGAN)上完善的，输入是一组图像对，如下图

pix2pix算法

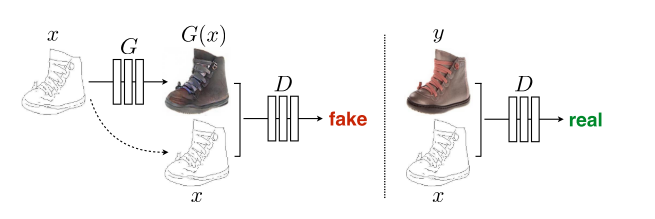
  • 转化域 $\boldsymbol X$ 、被转化域 $\boldsymbol Y$ : $\boldsymbol x \in \boldsymbol X,\boldsymbol y \in \boldsymbol Y$ , 完成转换 $\boldsymbol X \rightarrow \boldsymbol Y$

  • 生成器G : 根据输入的 $\boldsymbol x$ 生成虚假的图片 $G(\boldsymbol x)$

  • 判别器D : 判别$G(\boldsymbol x)$和$\boldsymbol y$的真假

生成器

我们的生成器的构架使用了U-net的

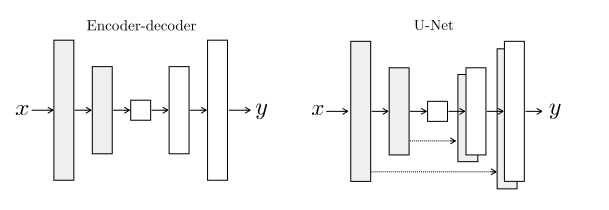
生成器结构

如上图，左图是一般的图像的信息提取模型，即编码器-解码器的构架，pix2pix算法使用的是一个变种的编码器-解码器，即U-Net。 具体地说，我们在每个层i和层n-i之间添加跳过连接，其中n是层的总数。 每个跳过连接只是将第i层的所有信道与第n-i层的信道连接起来。

判别器

判别器使用的是PatchGAN，事实上这个算法是根据局部识别来进行判别是否为真实的数据（将图片分成 $n \times n$ 份的小Patch作为输入），将所有的判别器的输出求其平均作为D的最终输出。

目标函数

目标函数可以沿用cGAN的目标函数

​ $\begin{aligned}
\mathcal{L}{c G A N}(G, D)=& \mathbb{E}{x, y}[\log D(x, y)]+\mathbb{E}_{x, z}[\log (1-D(x, G(x, z))]
\end{aligned}$

不过这里论文中多加了一个L1范式作为强制降低低频部分的正确率，最终我们可以得到目标函数

CycleGAN

论文主页 Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

简介

CycleGAN是基于pix2pix的一个算法，解决了pix2pix数据集必须成对限制，降低了对数据集的要求；解决的问题依旧是图像风格转化已经视觉风格转化的问题。下图是文中的Cycle示例。

CycleGAN的示例

理论基础

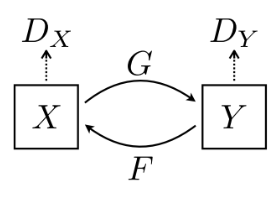
CycleGAN依然是解决图像转化的问题，其中这里不在需要成对的元数据来限制生成的图片，我们只需要两种不同风格的数据集（不需要成对匹配）即可。根据原始GAN的模型框架，在反方向叠加一个GAN构成CycleGAN如下图结构：

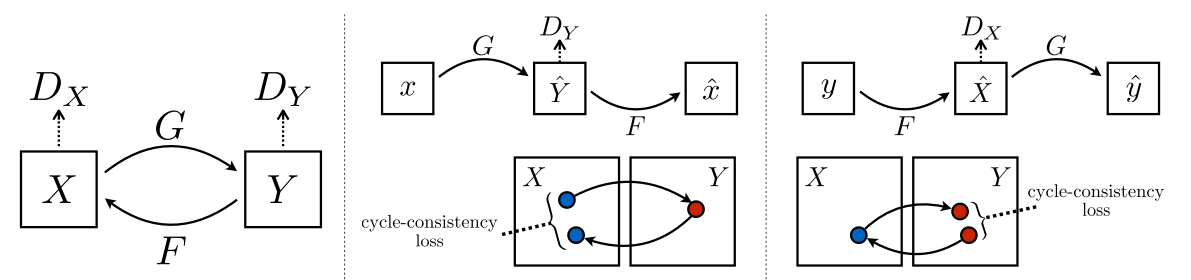
CycleGAN结构

我们只需要训练两个GAN模型如上图（中、右两部分）（$\hat x$、$\hat y$为生成器生成的数据）

  • 生成器$G$：$\hat y = G(x),x\in X$ ，表示讲$X$域的图像转到$Y$域的生成器；$ \hat y = G(\hat x)=G(F(y)),y \in Y$ 表示可以将 $F$ 生成的图片转换成生成前的图片
  • 生成器$F$： $\hat x = F(\hat y) = F(G(x)),x \in X$ 表示可以将 $G$ 生成的图片转换成生成前的图片；$F(y) = \hat x,y \in Y$,表示讲$Y$域的图像转到$X$域的生成器
  • 判别器$D_Y$：识别 $\hat y$ 是不是真实的$Y$域的图片
  • 判别器$D_X$：识别$\hat x$ 是不是真实的$X$域的图片

那么cycleGAN是如何控制好对于输入图片与输出图片的内容对应？上图中的有一个loss值为cycle-consistency loss，代表我们需要让上图中的$x$和$\hat x$ 以及 $y$和 $\hat y$ 的距离要尽可能小即最小化cycle-consistency loss这个值

生成器和判别器的模型结构我们可以模仿pix2pix的模型结构，在需要改变的地方微调模型即可，这里不再赘述

目标函数

  • 生成对抗损失

    • $G: X \rightarrow Y $ 的部分

    $\begin{aligned} \mathcal{L}{\mathrm{GAN}}\left(G, D_Y, X, Y\right) &=\mathbb{E}{y \sim p{\text {data }}(y)}\left[\log D_Y(y)\right]+\mathbb{E}{x \sim p_{\text {data }}(x)}\left[\log \left(1-D_Y(G(x))\right]\right.\end{aligned}$

    • $F:Y \rightarrow X$ 的部分

      $\begin{aligned} \mathcal{L}{\mathrm{GAN}}\left(F, D_X, Y, X\right) &=\mathbb{E}{x \sim p{\text {data }}(x)}\left[\log D_X(x)\right]+\mathbb{E}{y \sim p_{\text {data }}(y)}\left[\log \left(1-D_X(F(y))\right]\right.\end{aligned}$

  • 循环一致损失

    $\begin{aligned} \mathcal{L}{\text {cyc }}(G, F) &=\mathbb{E}{x \sim p{\text {data }}(x)}\left[|F(G(x))-x|_1\right]+\mathbb{E}{y \sim p_{\text {data }}(y)}\left[|G(F(y))-y|_1\right] \end{aligned}$

算法对比

pix2pix CycleGAN
数据要求 成对组型数据 不用成对
目标函数 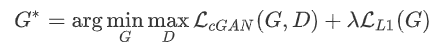image-20221120151936786
模型结构
方向 只能同时训练一个方向转换的模型 同时得到两个互转的模型