FOMM

Introduction

​ 本文章研究的是利用一个视频数据去驱动一个静态的图片，让其跟随 驱动视频 动起来。(这种驱动动画的技术可以用于 表情迁移 的研究方向上)，而对于驱动动画的技术，本篇文章算是一篇奠基的文章，后篇的关于驱动图片的文章大多是是以这个这个FOMM模型的部分改进创新。

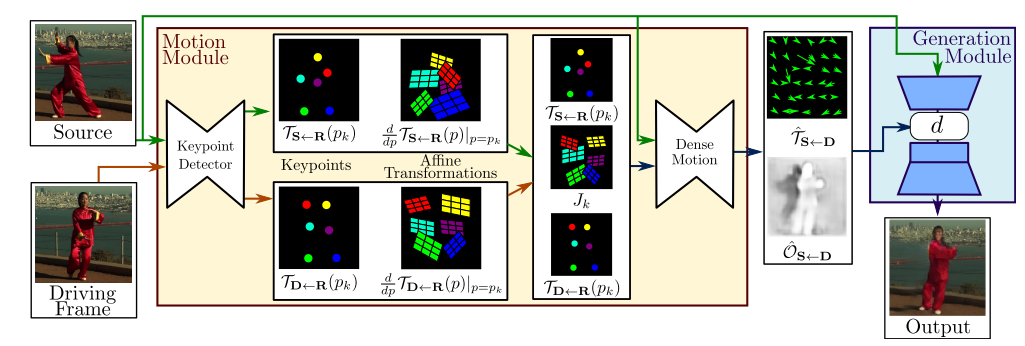
FOMM模型的具体内容如上图结构，该模型主要由两部分构成：运动模块（Motion Module）和生成模块（Generation Module）两部分组成。

Motion Module（运动模块）

作用：得到关键点流动映射 $\mathcal{\hat T}{S \leftarrow T}$ 和遮挡掩模 $\mathcal{\hat O}{S \leftarrow D}$

遮挡掩模指示 $D$ 的哪些图像部分可以通过扭曲源图像来重构以及哪些部分应当被修补，即从上下文推断

在本模块中，又包含两个部分： 关键点预测器 和 密度运动模块。这里我们注意，我们每一步处理的都是原图（Source）和驱动帧（Driving Frame）（驱动视频的某一帧）。

其中 关键点预测器 是直接作用在两张图片的，得到最终的图片的关键点信息 $\mathcal T{S \leftarrow R}$ 和 $\mathcal T{D \leftarrow R}$ (关键点表示充当导致紧凑运动表示的瓶颈)和每一组仿射变换的参数。

我们假设存在一个抽象参照系 $R$ 因此，估计 $\mathcal T{S \leftarrow D}$包括估计 $\mathcal T{S \leftarrow R}$和 $\mathcal T{D \leftarrow R}$。此外，给定帧 $X$ ，我们估计学习的关键点邻域中的每个变换 $\mathcal T{X \leftarrow R}$ 给定变换$\mathcal T_{X \leftarrow R}$，我们考虑它在$K$个关键点 $p_1 …. p_k$ 。这里，$p_1 …. p_k$ 表示关键点在参考帧 $R$ 中的坐标。

$$\mathcal T_{\mathbf{X}\leftarrow\mathbf{R}}(p)=\mathcal T_{\mathbf{X}\leftarrow\mathbf{R}}(p_{k})+\left({\frac{d}{d p}}{\mathcal{T}}_{\mathbf{X}\leftarrow\mathbf{R}}(p)\Big|_{p=p_{k}}\right)(p-p_{k})+o(||p-p_{k}||)$$

注意：$p$ 代表参考帧 $R$ 的位置点，$z$ 为$X$、$S$ 或者 $R$ 的位置点。

$$\mathcal T_{\mathbf{X}\leftarrow\mathbf{R}}(p) \backsimeq \{ \{ \mathcal T_{X \leftarrow R}(p_1), \frac{d}{dp} \mathcal T_{X \leftarrow R}(p) \Big \vert_{p=p_1} \},...,\{ \mathcal T_{X \leftarrow R}(p_k), \frac{d}{dp} \mathcal T_{X \leftarrow R}(p) \Big \vert_{p=p_k} \} \}$$

为了估计 ${\mathcal{T}}{\mathbf{R}\leftarrow\mathbf{X}}={\mathcal{T}}{\mathbf{X}{\leftarrow\mathbf{R}}}^{-1}$ ,文章中假设$\mathcal T{X \leftarrow R}$在每个关键点的邻域内是局部双射的。需要在 $D$ 中的关键点 $z_k$ 附近估计 $\mathcal{T}{S \leftarrow T}$，假定 $zk$ 是对应于 $R$ 中的关键点位置 $p_k$ 的像素位置。为此，我们首先估计驱动标架 $D$ 中的点 $z_k$ 附近的变换$\mathcal T{R←D}$, 即 $pk = \mathcal T{R←D}(zk)$, 然后估参考 $R$ 中 $p_k$ 附近的变换 $T{S←R}$

$$\mathcal{T}_{\mathrm{S}\leftarrow\mathrm{D}}=\mathcal{T}_{\mathrm{S}\leftarrow\mathrm{R}}\circ\mathcal{T}_{\mathrm{R}\leftarrow\mathrm{D}}=\mathcal{T}_{\mathrm{S \leftarrow R}}\circ\mathcal{T}_{\mathrm{D\leftarrow R}}^{-1}$$

上述是计算 $\mathcal{T}_{\mathrm{S}\leftarrow\mathrm{D}}$ 的逻辑过程，经过推到后，可以利用下面的公式进行代码编写计算：

$${\mathcal{T}_{\mathrm{S}\leftarrow\mathbf{D}}}(z)\approx{\mathcal{T}_{\mathrm{S}\leftarrow\mathbf{R}}}(p_{k})+J_{k}(z-{\mathcal{T}_{\mathrm{D}\leftarrow\mathbf{R}}}(p_{k}))$$

其中 $J_k$ 为：

$$J_{k}=\left(\frac{d}{d p}\mathcal{T}_{\mathrm{S}\leftarrow\mathrm{R}}(p)\Bigl|_{p=p_{k}}\right)\left(\frac{d}{d p}\mathcal{T}_{\mathrm{D}\leftarrow\mathrm{R}}(p)\Bigl|_{p=p_{k}}\right)^{-1}$$

为了结合局部运动，文章中使用了卷积神经网络进行的估计实际的变化矩阵，但是由于$T{S ← D}$将 $D$ 中的每个像素位置映射到 $S$ 中的对应位置，因此 $T {S ← D}$ 中的局部模式（如边缘或纹理）与 $D$ 对齐，但与 $S$ 不对齐。因此，文章中利用上述计算所获得的局部变换$\mathcal T{S \leftarrow D}$获得 $K$ 个变换图像$S_1,…,S_K$，每个$S_K$在关键点的邻域中与 $T{S ← D}$ 对齐，用于背景的附加图像$S_0 = S$。

对于每个关键点 $pk$，我们另外计算热图 $H_k$，其向密集运动网络指示每个变换发生的位置。每个$H_k(z)$被实现为以$T{D ← R}(pk)$和$T{S ← R}(p_k)$ 为中心的两个热图的差：

$$\mathbf{H}_{k}(z)=e x p\left({\frac{(\mathcal T_{\mathrm{D}\leftarrow\mathbf{R}}(p_{k})-z)^{2}}{\sigma}}\right)-e x p\left({\frac{(\mathcal T_{\mathrm{S}\leftarrow\mathbf{R}}(p_{k})-z)^{2}}{\sigma}}\right), σ = 0.01$$

热图 $Hk$ 和变换图像 $S_0，…,S_K$由U-Net 连接和处理。$T{S ← D}$使用上述方法进行估计。我们假设一个物体由 $K$ 个刚性部分组成，并且每个部分按照$\mathcal T{S \leftarrow D}$. 因此，我们估计$ K+1 $个掩码$M_k，k = 0,…,K$，其指示每个局部变换在何处成立。最终的密集运动预测$\mathcal {\hat T}{S ← D}(z)$由下式给出：

$$\hat{\mathcal{T}}_{\mathrm{S}\leftarrow\mathbf{D}}(z)=\mathbf{M}_{0}z+\sum_{k=1}^{K}\mathbf{M}_{k}\left(T_{\mathbf{S}\leftarrow\mathbf{R}}(p_{k})+J_{k}(z-T_{\mathbf{D}\leftarrow\mathbf{R}}(p_{k})\right))$$

​ 源图像 $S$ 与要生成的图像 $\hat D$ 不是逐像素对齐的。为了处理这种未对准，文中使用特征扭曲策略。在S中存在遮挡的情况下，光流可能不足以产生D。实际上，S中被遮挡的部分不能通过图像扭曲来恢复，因此应该进行修补。因此，我们引入一个遮挡图 $\mathcal {\hat O}_{S←D} \in [0，1]^{H ×W}$ 来屏蔽掉需要修复的特征图区域。遮挡掩模减小了对应于遮挡部分的特征的影响。

$$\boldsymbol \xi^{\prime} = \mathcal{\hat O}_{S \leftarrow D} \odot f_w(\xi,\mathcal {\hat T}_{S ← D})$$

其中 $f_w(.,.)$ 表示反扭曲运算，$\odot$ 表示阿达玛乘积。

密度运动模块的作用就是我们上述所述的，利用相对参考帧 $R$ 的关键点以及一阶导数计算全局变换的$\mathcal{\hat T}{S \leftarrow T}$ 和 遮挡掩模 $\mathcal{\hat O}{S \leftarrow D}$

Generation Module（图像生成模块）

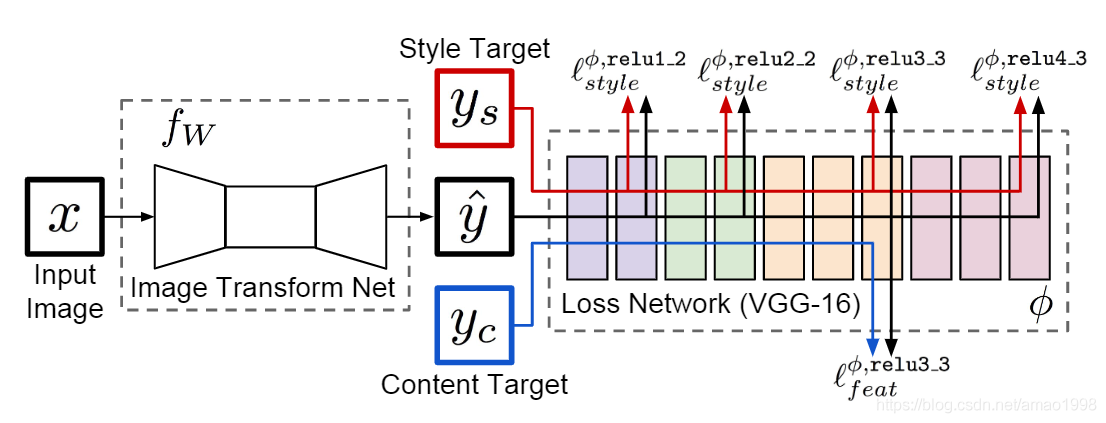
Training Losses

• 使用预先训练的VGG-19网络作为我们的主要驱动损失

$${\cal L}_{r e c}(\hat{\bf D},{\bf D})=\sum_{i=1}^{I}\left|N_{i}({\bf\hat{D}})-N_{i}({\bf\hat{D}})\right|$$

其中 $N_i(·)$ 是从特定VGG-19层提取的第 $i$ 个特征通道变换层，$I$ 是该层中的特征层数量。

Imposing Equivariance Constraint

我们假设图像X经历已知的空间变形$T{X←Y}$。在这种情况下，$T{X←Y}$可以是仿射变换或薄平面样条变形。在该变形之后，我们获得新的图像$Y$。现在，通过将我们的扩展运动估计器应用于这两幅图像，我们获得了 $T{X←R}$ 和 $T{Y←R}$ 的一组局部近似。标准约束写为：

$$\mathcal T_{X \leftarrow R} \equiv \mathcal T_{X \leftarrow Y} \circ T_{Y \leftarrow R}$$

在计算两侧的一阶泰勒展开式之后，获得以下约束:

$$\begin{array} \mathcal T_{X \leftarrow R}(p_k) \equiv \mathcal T_{X \leftarrow Y} \circ T_{Y \leftarrow R}(p_k)\\ \\ (\frac{d}{dp} \mathcal T_{X \leftarrow R}(p) \Big |_{p=p_k}) \equiv (\frac{d}{dp} \mathcal T_{X \leftarrow Y}(p) \Big |_{p=\mathcal T_{Y \leftarrow R}(p_k)})(\frac{d}{dp} \mathcal T_{Y \leftarrow R}(p) \Big |_{p=p_k})\\ \end{array}$$

我们将上述式子进行变形可以得到：

$$\mathbb{1} \equiv (\frac{d}{dp} \mathcal T_{X \leftarrow R}(p) \Big |_{p=p_k})^{-1} (\frac{d}{dp} \mathcal T_{X \leftarrow Y}(p) \Big |_{p=\mathcal T_{Y \leftarrow R}(p_k)})(\frac{d}{dp} \mathcal T_{Y \leftarrow R}(p) \Big |_{p=p_k})$$

以上就是我们训练过程中对于生成关键点的约束方程。